引言:折纸和算盘作为折叠纸张的艺术和计算的工具,具有几百甚至上千年的历史,时至今日,折纸更是在生物医学、航天等领域得到了广泛应用,那你有没有想过折纸还可以像算盘一样用来计算,甚至是全自动数字式的算盘?
近日,俄亥俄州立大学赵芮可教授团队和佐治亚理工学院Glaucio H. Paulino教授团队在《美国国家科学院院刊》(PNAS)上在线发表题为“Untethered control of functional origami micro-robots with distributed actuation”的论文,就让这个想法成为了可能。作者将磁响应材料和双稳态Kresling型折纸结构结合构成一种新型的多功能驱动器,若将每个驱动单元想象成一个算珠,展开状态时记数为1,一方面,通过单一外加磁场的控制即可实现多个驱动单元的独立控制,功能类似于手拨算珠,另一方面,双稳态的结构可用于信息存储,便于读出算盘上最终记录的结果。
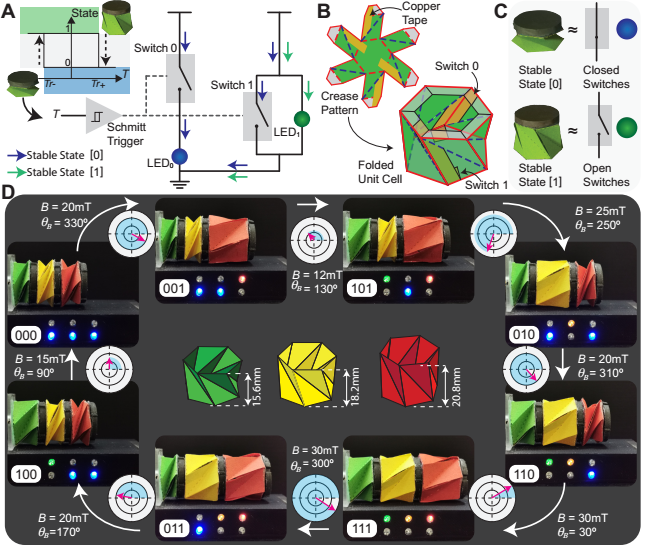
从现代数字计算角度考虑,双稳态Kresling驱动器具有与施密特触发器类似的特性,作为一个可折叠结构,将输入转矩看成输入信号,机械状态看成输出信号(展开状态为二进制输出1,折叠状态为二进制输出0),则输入转矩与输出数字状态0和1之间具有固定的关系,可以实现相似的模数转换和信息存储功能(如图二和视频一中展示的三位存储器,各单元的独立驱动实现存储信息的改变,LED实时显示存储的信息)。另外,Kresling驱动器还可以通过自身状态的变化被动的反应出外界负载的大小并通过磁驱动主动的做出响应,因此集成了驱动、传感和计算的功能于一体,完美契合机器人所需要的感应-决策-响应的所有功能,是新一代智能机器人系统的潜在方案。
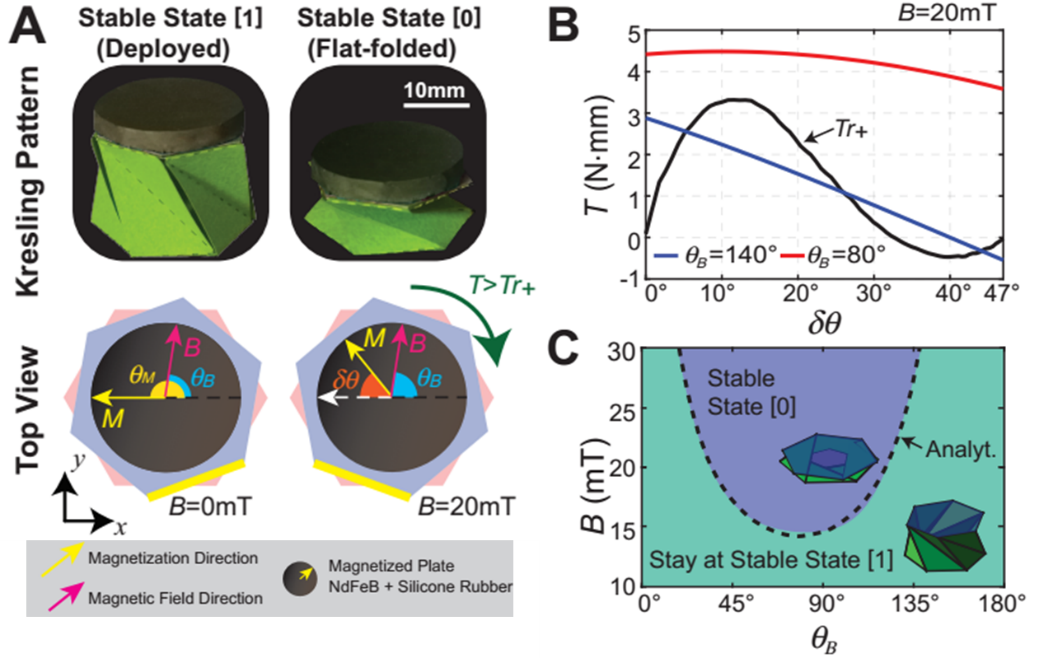
Kresling驱动单元的原理如图三所示,折纸结构顶端固定有磁化后的磁片,若外加磁场的方向与磁片的磁化方向不同,将产生趋向于磁场方向的转矩,通过控制磁场的方向和大小,当磁转矩在驱动单元旋转的过程中始终大于所需要克服的转矩 (图三C中的紫色区域),则驱动单元可以克服折纸结构的能量壁垒,在折叠状态和展开状态之间快速切换 (视频二)。
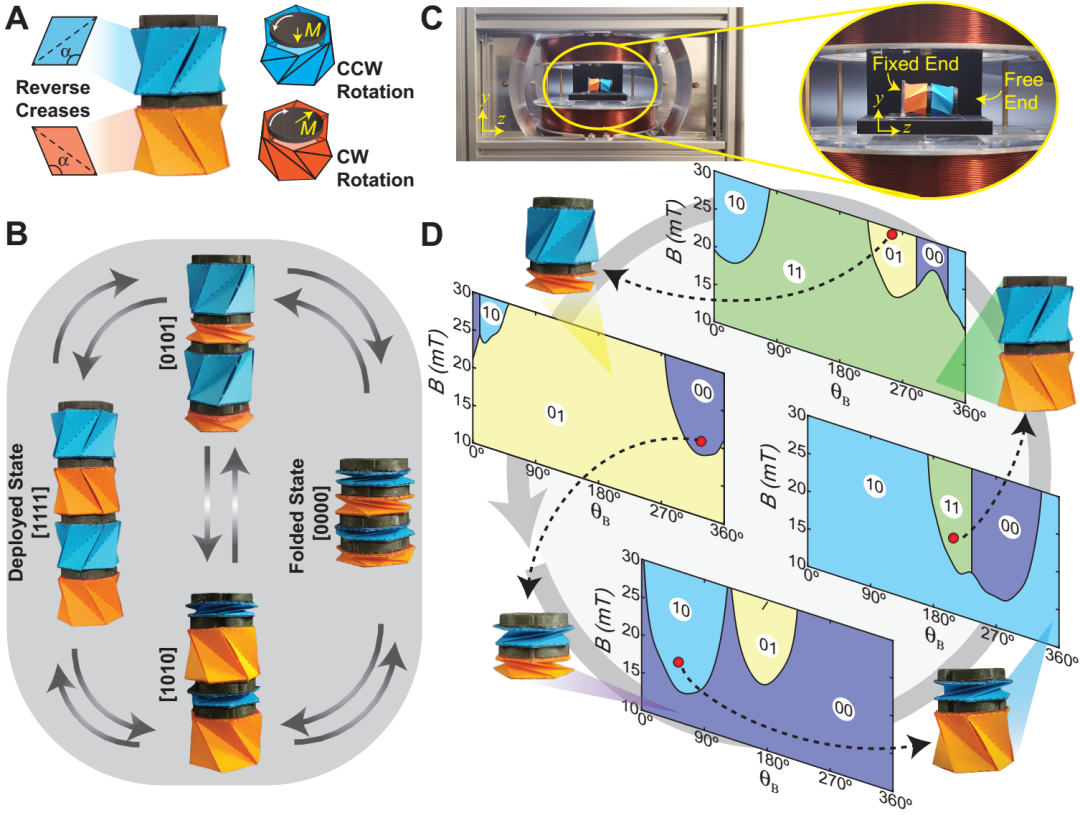
当多个驱动单元组装在一起,通过设计各单元上磁片的磁化方向的不同并调节外加磁场的大小和方向,各单元所受转矩的大小和方向均不同,可以实现装配体各单元的同时驱动和独立分布式控制(distributed actuation)。例如图四和视频三中所示,由两个相同单元组成的装配体,在完全折叠状态下,上下两个磁片的磁化方向相差90°,装配体可以从完全折叠状态驱动为其他三种状态。
基于分布式控制的原理,当Kresling驱动器装配体变为另外一个状态后,各单元上磁片的磁化方向也相应的发生变化,此时驱动所需的磁场方向和大小也会发生变化,通过合理设计和计算,装配体在任意状态之间可以实现直接或者间接的快速切换。(图五和视频四)。

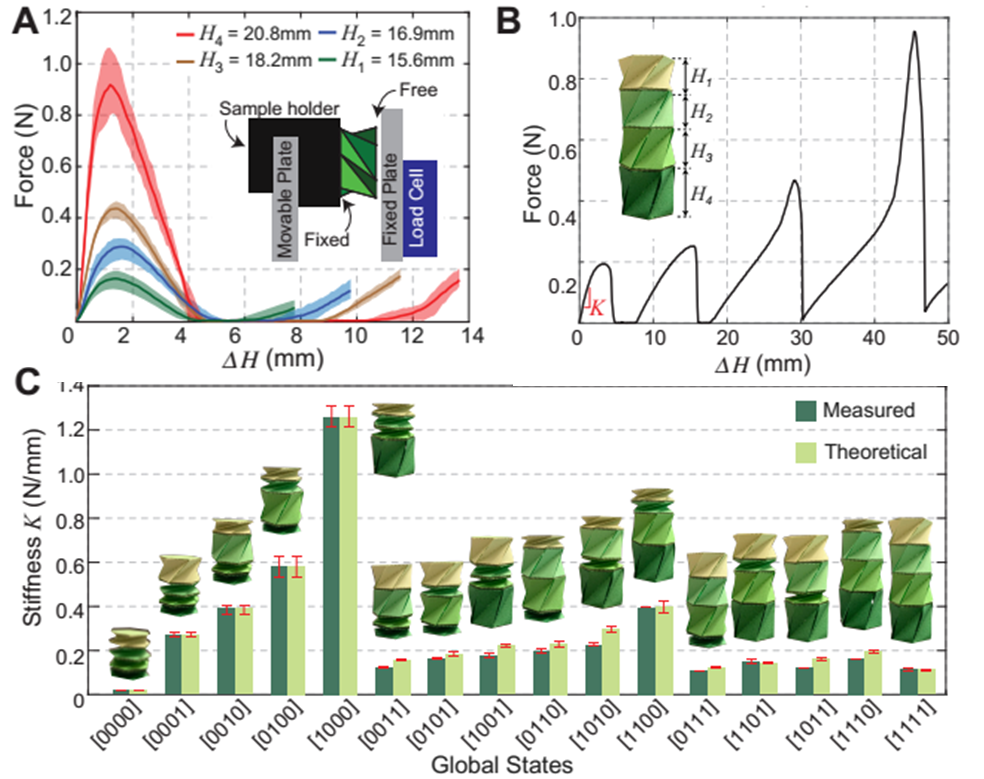
研究团队还进一步研究了Kresling型驱动器各单元独立控制并协同作用带来的其他潜在应用。对于驱动单元,通过对折纸结构的设计可以获得不同的能量壁垒,具体到本文,折纸高度越高则能量壁垒越大。当四个高度不同的单元层叠成装配体时,由于每个单元的刚度均不同,装配体结构可以随着状态的切换获得16种不同的刚度特性,配合磁驱动可以用来设计刚度快速可调的阻尼器。
团队成员表示希望下阶段的工作可以实现驱动器的运动,结合集成的传感和计算功能,将磁驱动折纸应用在智能机器人领域。
本文通过结构的双稳态特性实现了形状锁定(shape-locking),赵芮可教授团队和佐治亚理工的齐航教授团队今年还通过设计一种新的材料,即磁驱形状记忆高分子(Magnetic shape memory polymer, M-SMP)来实现形状锁定,该材料可通过控制磁加热和磁驱动实现低温形状锁定和高温快速变形,相关成果发表在《先进材料》(Advanced Materials)上,
团队介绍
该工作由俄亥俄州立大学软智能材料实验室(Soft Intelligent Materials Laboratory,链接: http://zhaor.engineering.osu.edu)和佐治亚理工学院计算力学实验室(Prof. Glaucio H. Paulino’s Computational Mechanics Research Group,链接: http://paulino.ce.gatech.edu/index.html)共同完成。该工作的通讯作者为赵芮可教授和Glaucio H. Paulino教授,共同第一作者为佐治亚理工学院博士生Larissa S. Novelino,俄亥俄州立大学博士后迮弃疾博士,以及俄亥俄州立大学博士生吴帅。
论文链接:


