毛细现象泛指与液体表面张力和浸润性相关的一系列现象. 最典型的例子就是毛细升现象(capillary rising): 将细小的玻璃管插入水中,水会在管中上升到一定高度才停止. 毛细升现象的驱动力, 是玻璃和水之间相互吸引的相互作用, 也就是我们常说的毛细力. 而阻碍水上升的因素有两个: 一个是水在管中流动受到的黏滞阻力, 另一个就是水的重力. 在毛细升的初始阶段, 当水的高度比较小, 重力作用可以忽略时, 只剩下毛细力和黏滞阻力之间的竞争, 水的高度和时间之间满足1/2的标度关系, ht1/2. 这个就是著名的Lucas-Washburn定律.

还有一类毛细现象同样有趣, 但可能大家不太熟悉. 将两块亲水的平板相交成锐角, 然后垂直的插入水中. 同样在毛细力的作用下, 水会在两块平板的夹角间迅速上升. 达到平衡后, 从侧面看观察会发现水的液面为双曲线形. 这个现象叫作泰勒升(Taylor rising). 第一个发现这个现象的泰勒, 正是大学数学中学到的泰勒展开的那位泰勒. 在几何构型成夹角中的毛细现象在大自然中同样是普遍存在的, 而且大自然运用毛细作用的精巧程度往往让人叹为观止. 比如在猪笼草表面液体的单向输运, 和瓶子草鞭毛鞭毛表面液体的快速铺展, 都借助了有夹角情况下的毛细力.
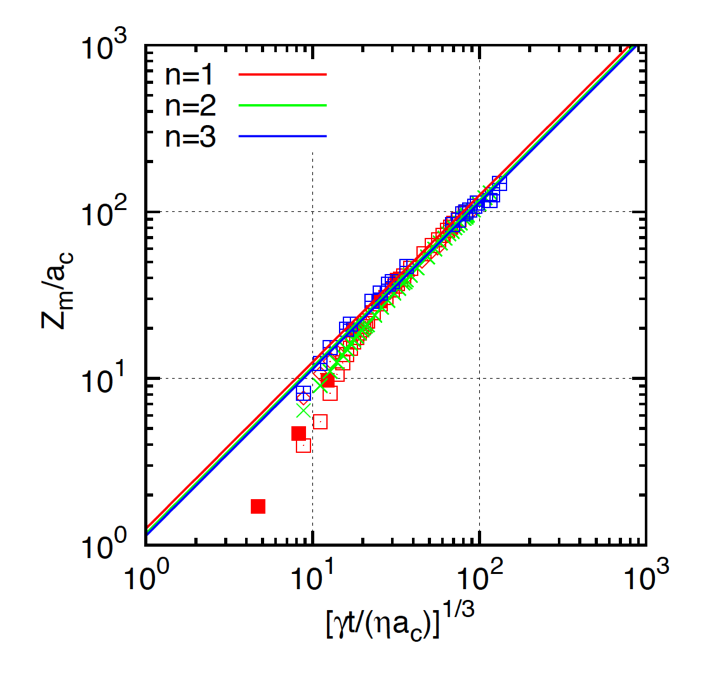
那么泰勒升的动力学演化过程, 是否也存在和Lucas-Washburn定律类似的标度关系呢? 这个问题的答案, 在1994年的时候汤雷翰老师(香港浸会大学)就已经给出. 的确, 泰勒升中水的前端随时间满足t1/3的标度关系. 这个标度关系表明泰勒升比毛细升一开始的t1/2要慢, 但比毛细升后期要快, 因为毛细升最终会达到一个平衡高度, 而泰勒升则会一直进行下去.
2011年, 法国巴黎高等物理化工学院的研究者更进一步. 他们把形成夹角的平面推广到了更加一般的幂率弯曲表面(y=xn, n=1对应的是平面). 实验中发现, 对于不同的幂率表面, 只要夹角比较小, 泰勒升的动力学都是满足1/3次方的标度关系. 这个时候, 做物理的人对这个体系开始感兴趣了, 因为物理学关注的正是这种在不同体系中出现的普适性规律.
在最新的一期Journal of Fluid Mechanics 中, 北京航空航天大学的周嘉嘉副教授和土井正男教授合作, 系统的研究了不同幂率条件下泰勒升的动力学问题. 他们采用的方法是昂萨格变分原理(Onsager variational principle), 这种方法是推导非平衡态动力学演化方程的系统性方法, 感兴趣的同学可以参考土井老师的Soft Matter Physics一书. 运用润滑近似, 他们推导出了泰勒升中液面随时间变化应该满足的一个偏微分方程. 通过数值求解发现, 液体前端和时间之间的确存在1/3的标度关系.
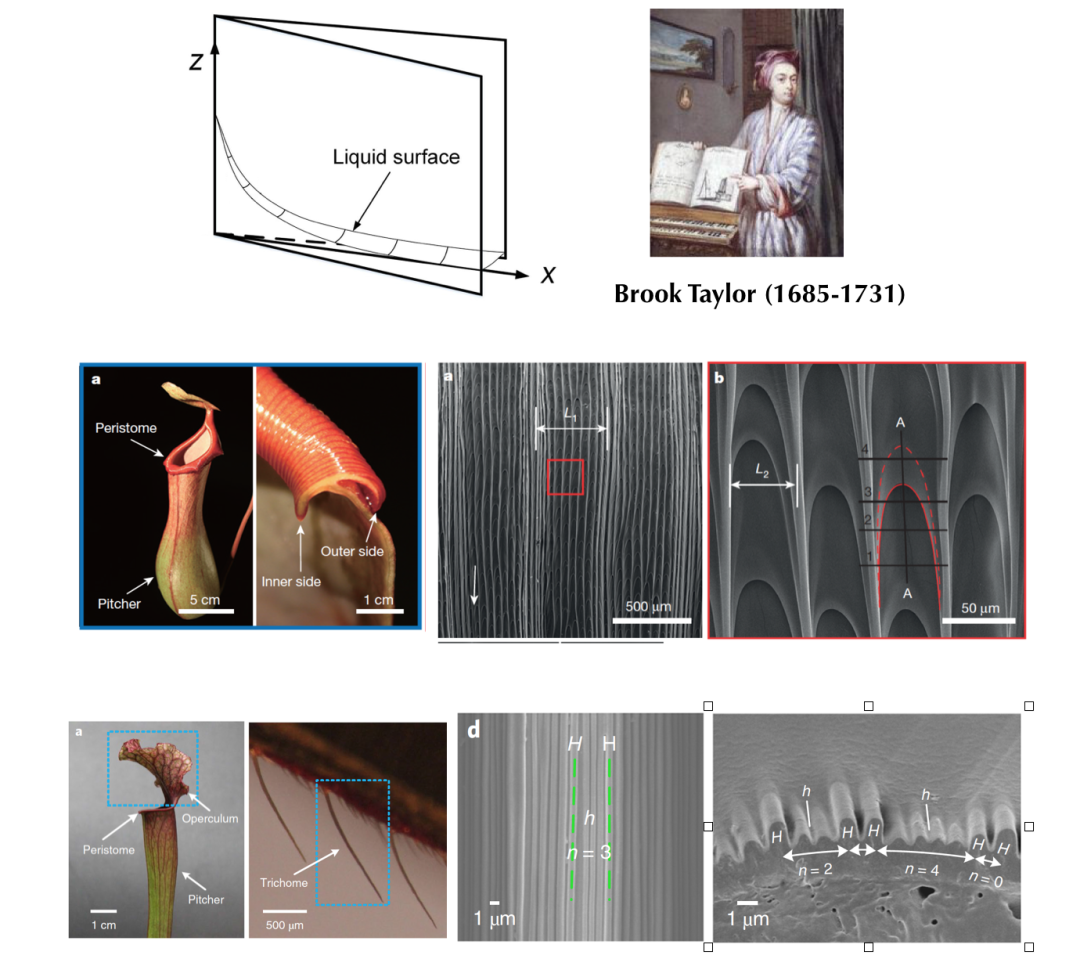
数值计算的结果的确证实了1/3的标度关系, 但是否能更进一步证明这个标度关系呢? 泰勒升现象中还有一个特点, 就是在这个体系中没有一个特征长度. 对比毛细升现象, 毛细管的内径则是毛细升现象中的一个确定的特征长度. 在数学的角度看, 缺乏特征长度的动力学体系有可能存在自相似(self-similar)的特性. 自相似是指几何物体之间虽然大小不一, 但都具有相同的形状, 一个典型的例子就是俄罗斯套娃: 每个娃娃形状是一样的, 只是大小不同.

回到泰勒升的问题, 由于体系存在的自相似性, 通过选取一个随时间变化的长度来约化液面演化的偏微分方程, 可以得到一个与时间无关的常微分方程, 而这个常微分方程的解则决定了液面的形状. 泰勒升中不同时刻的液面, 通过这个变化, 可以完全重合到一条曲线上去. 而能够实现这个变换的约化长度, 正好是和时间成1/3次方的关系.
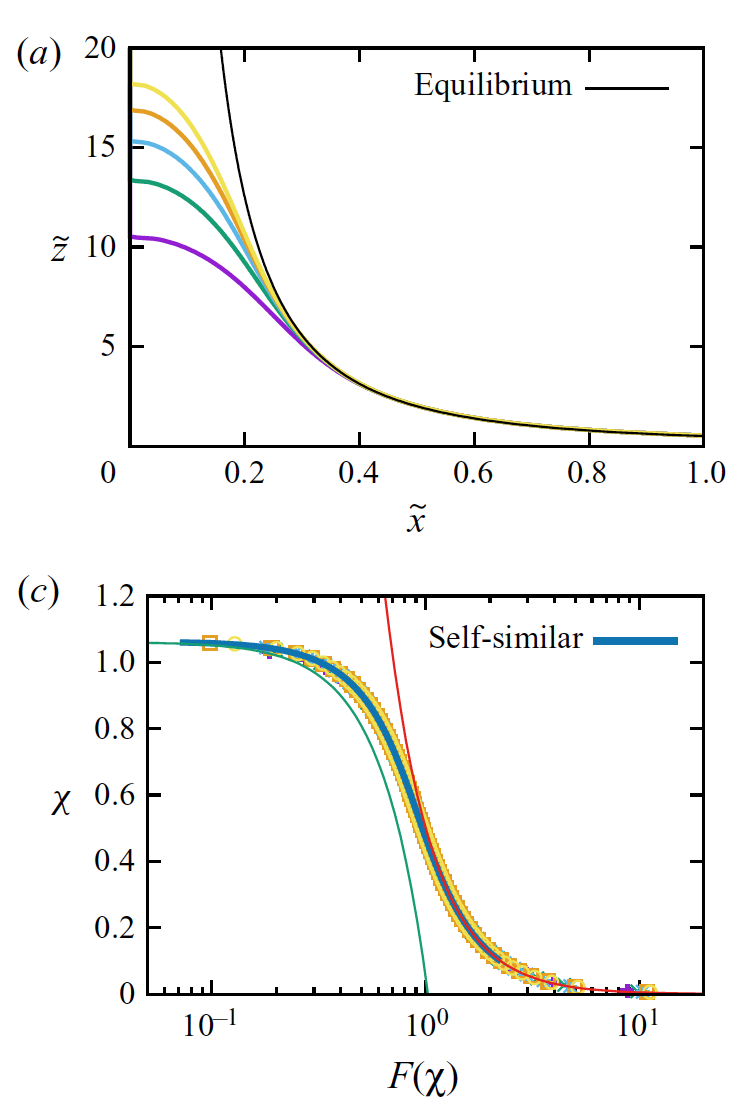
文章最后还存在一个小小的疑惑. 在法国研究者的实验中发现, 如果选用毛细长度(capillary length)对实验数据做无量纲化, 液体前端随时间的变化满足h=C*t1/3关系. 对于不同幂率的泰勒升, 不但标度指数1/3是普适的, 关系中的系数C同样也是普适的, 其数值大小对不同幂率基本上一样. 自相似计算的结果也确认了这个结论, 但是否能够严格证明, 还有待进一步的探索. 该研究工作受到国家自然基金的支持.
论文链接:
https://doi.org/10.1017/jfm.2020.531
相关研究:
Tang and Tang, J. Phys. II 1994, 4, 881. DOI: 10.1051/jp2:1994172 Ponomarenko, Quere, and Clanet, J. Fluid Mech. 2010, 666, 146. DOI: 10.1017/s0022112010005276


