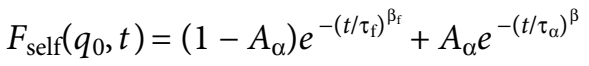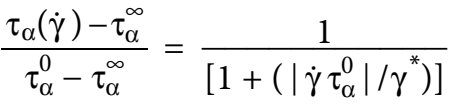聚合物熔体在加工过程中会发生剪切变形和流动,从而导致其松弛动力学发生显著的变化。许多研究表明,随着材料的变形,结构松弛时间和有效粘度会降低,有时这种降低达到几个数量级。经过长时间的“老化”后,变形流体的松弛动力学恢复至平衡状态。虽然有大量的实验研究报道,但从理论角度阐述聚合物熔体松弛动力学的变化仍然很困难。
成果介绍
基于以上分析,美国国家标准技术研究所Jack F. Douglas教授课题组基于分子动力学模拟,提出了一种稳态剪切下粗粒聚合物熔体的α松弛动力学模型。发现剪切力会逐渐抑制聚合物熔体的α松弛过程,最终导致在高剪切速率下纯惯性β松弛占据主导地位,这种趋势类似于升高温度。随着剪切速率的增加,熔体粘度下降了2~4个数量级,在高剪切速率下熔体粘度与温度无关。剪切变稀是由于在剪切作用下,大分子之间的瞬间缔合发生了“解聚”或者固定的颗粒团簇被破坏造成的。
聚合物熔体模拟方法
为了研究聚合物熔体在稳态剪切下的动力学松弛过程,研究者采用分子动力学进行模拟,使用LAMMPS代码进行计算。通过谐波弹簧连接的珠子组成的完全柔性链表示聚合物,每条聚合物链有20个单体,模拟时聚合物链个数为500个,总共10,000个单体,分子间作用力通过截断的LJ相互作用势表示。模拟初始时采用Nose-Hoover恒温器和恒压器使系统在NPT系综中平衡(恒定数量的粒子N,压力P和温度T),平衡后,在xy平面上以固定剪切速率将剪切变形作用于模拟单元。模拟采用周期性边界条件,温度范围从T = 0.43到T = 0.55,剪切速率范围从10-5到100。每个状态下对十二个独立副本进行计算以获取统计平均值。
聚合物熔体的剪切变稀效应
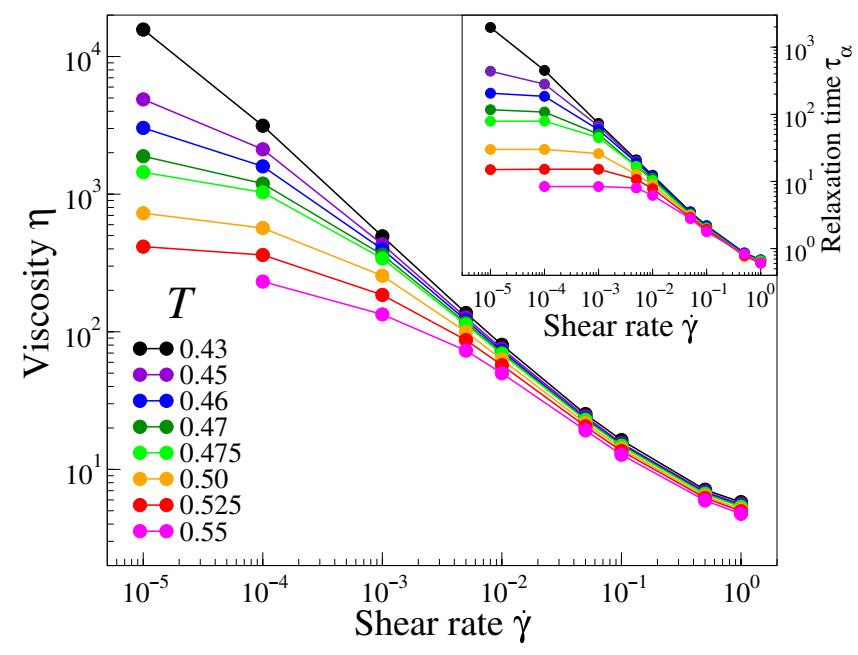
研究者研究了聚合物熔体粘度和结构松弛时间随剪切速率的变化关系。当剪切速率最低时,聚合物熔体达到平衡粘度,随着剪切速率的增加,熔体粘度下降了2~4个数量级,而且在高剪切速率下熔体粘度的温度依赖性几乎消失。
剪切变稀是复杂流体中的常见现象。他们认为剪切变稀是由于在剪切作用下流体结构被破坏,大分子之间的瞬间缔合发生了“解聚”或者叫做固定颗粒团簇被破坏造成的。
聚合物熔体的松弛时间
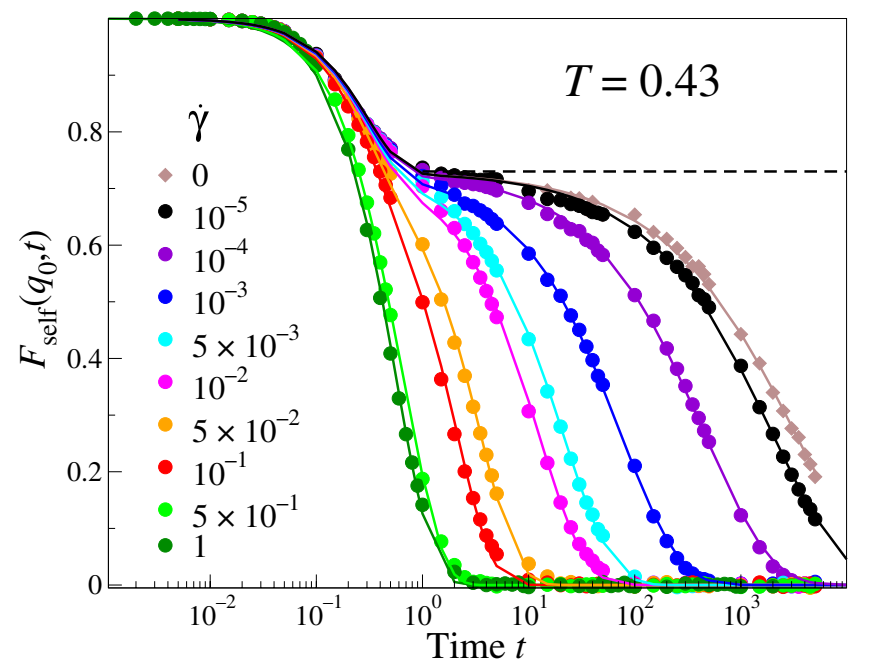
研究者研究了最低温度下的中间散射函数在不同剪切速率下随时间的变化关系。发现随着剪切速率增加,α松弛被抑制,α松弛时间降低,最终α松弛和快速γ松弛融合在一起,这与增加温度达到的效果一致。为了量化这些结果,他们采用如下方程对数据进行拟合:
该式中中间散射函数分为两部分:β松弛(松弛时间与温度无关)和α松弛(松弛时间与温度相关,振幅与温度无关)。
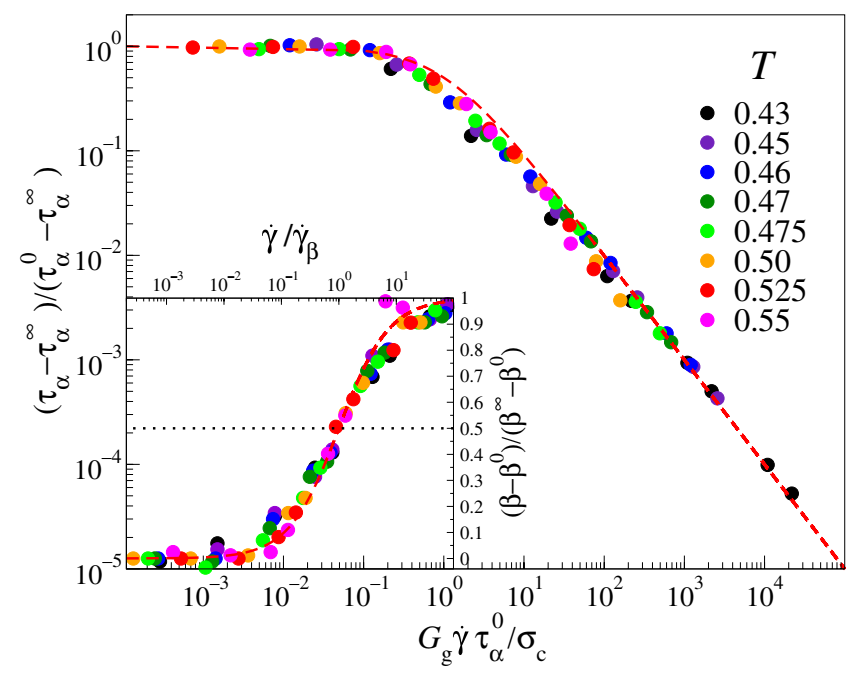
临界流体动态重整化群理论表明粘弹性松弛时间描述了与初始相分离有关的动态粒子簇的寿命,在稳定剪切作用下这些团簇逐渐破裂。当没有达到稳态剪切的情况下,近临界流体的剪切粘度和法向应力以相关长度的幂的形式发散,该相关长度描述了动态粒子簇的平均大小。
他们在模拟中发现α松弛时间随着剪切速率的增加而降低,在临界剪切速率下逐渐与β松弛融合。这意味着在高剪切速率下α松弛时间必须近似等于,而为属于温度不敏感的松弛时间,为了解决这种限制,研究者采用如下的简化形式:
当剪切强度趋于无穷时的松弛时间为0.5时可以很好的拟合实验数据,这是由于无量纲时间单位约为1 ps,与接近的缘故。
聚合物熔体簇的破裂
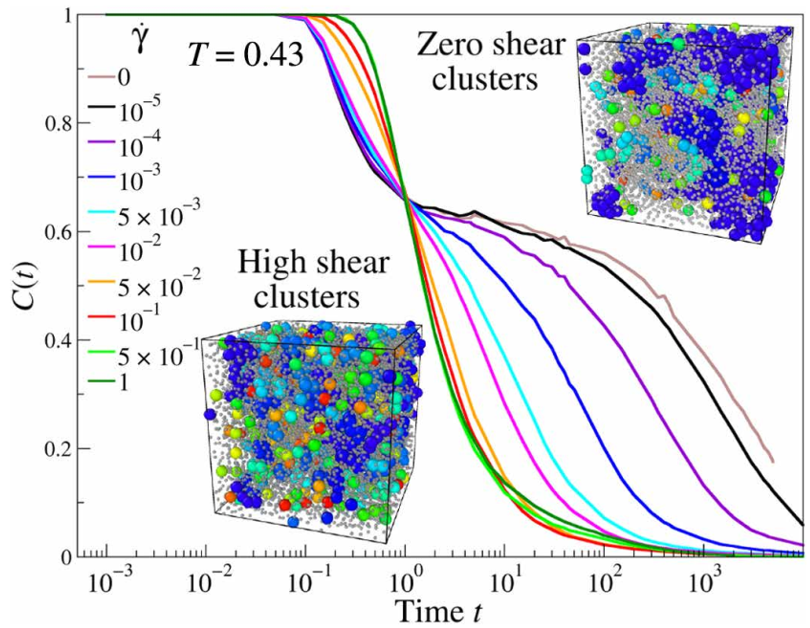
Starr等人定义了一个自相关函数,该函数定义了固定颗粒保持“笼形”状态的持久性。研究者采用了这一函数,研究了剪切是如何改变固定颗粒簇的持续时间,得出了笼形颗粒的分数与剪切速率的关系。
与变温条件下不动团簇寿命的平衡分析一致,其衰减时间与结构弛豫时间相当,并且随着剪切速率的增加而变短。研究者还给出了在高剪切和零剪切条件下的系统快照。尽管平衡系统显示出较大的固定粒子簇,但实际上随着剪切速率的增加,它们逐渐分解为更小且空间上更不均匀的簇,其效果与平衡时增加温度相当。
聚合物熔体的稳态极限流动
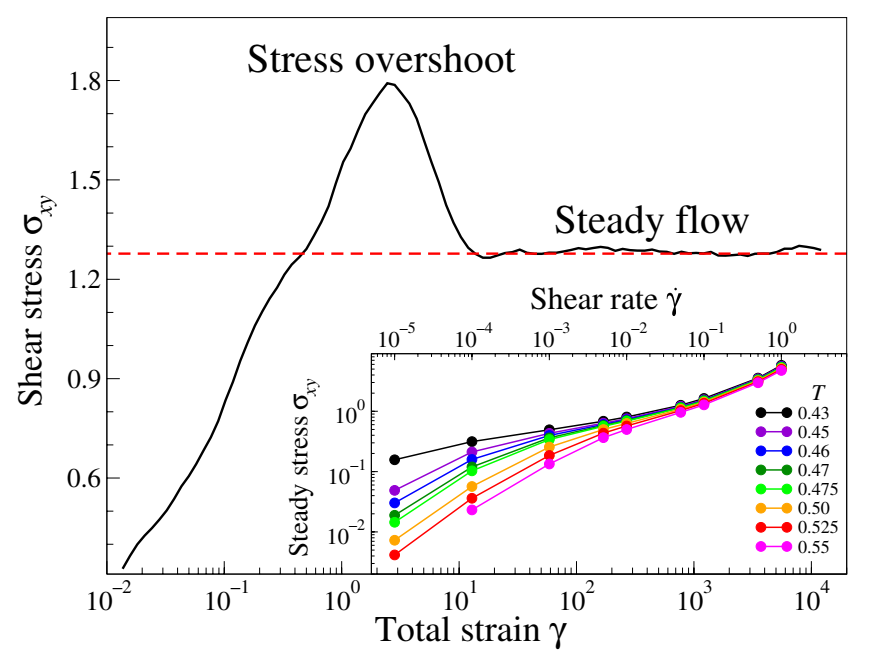
研究者研究了稳态流动下聚合物熔体的极限行为。发现在T = 0.55、剪切速率为10-1时,系统的剪切应力随总应变增加而增加,随后趋于平稳。初始线性增加后,剪切应力发生了应力过冲,最大值发生在总应变2.6附近。应力下降后,可以观察到稳定的流动,系统建立了准平衡。在低剪切速率下稳态应力与温度有关,而当剪切率高于10-1时这种相关性消失。
小结
为了阐明在稳态条件下聚合物熔体松弛行为,美国国家标准技术研究所Jack F. Douglas教授课题组基于分子动力模拟,研究了熔体松弛时间与剪切速率的关系,从分子运动角度阐述了聚合物熔体的剪切变稀行为。发现随着剪切速率的增加,熔体粘度下降了2~4个数量级,在高剪切速率下熔体粘度与温度无关。剪切变稀是由于在剪切作用下,大分子之间的瞬间缔合发生了“解聚”或者叫固定的颗粒团簇被破坏造成的。随着剪切速率增加,α松弛被抑制,最终与快速γ松弛融合在一起。系统的剪切应力在初期随总应变线性增加,在总应变2.6附近发生了应力过冲,随后系统达到了准平衡状态。
原文链接: